Resolver sistemas de ecuaciones

Resolver Sistemas de Ecuaciones Online (sistemas lineales y no lineales)

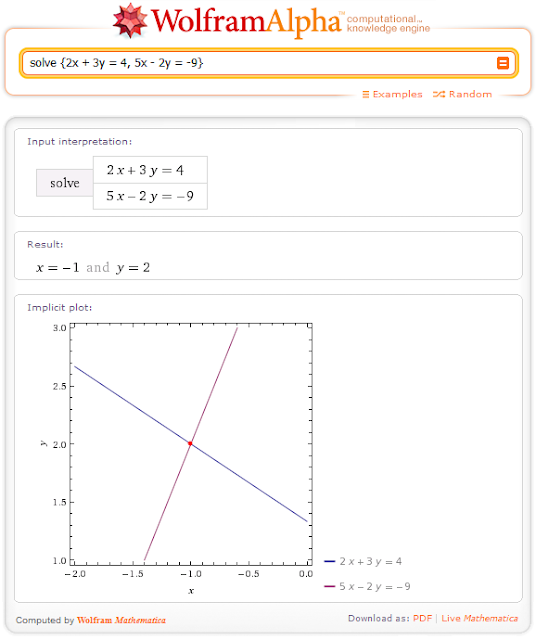
Resolver el siguiente sistema de ecuaciones lineales (2x2):

2x + 3y = 4

5x - 2y = -9

La solución en video:


La solución online utilizando WolframAlpha: Primero ingresamos a la página de WolframAlpha:

Luego, debemos ingresar en la caja de texto lo siguiente: solve {2x + 3y = 4, 5x - 2y = -9} presionamos  la tecla enter y la respuesta que obtendremos será la siguiente:

En la primera parte (Input interpretation) aparece el sistema de ecuaciones que hemos ingresado, debemos revisar si esta deacuerdo con lo que deseamos resolver (a veces aparecen errores debido a que es un poco dificil escribir una ecuación en forma de texto). Luego nos aparece el resultado y un gráfico de la solución. Veamos más ejemplos.

Resolver el siguiente sistema de ecuaciones lineales (3x3)

2x - y - 4z = 12

3x - 4y + 2z = -11

-5x + 2y - z = 2

La solución en video:


La solución online utilizando WolframAlpha:
Debemos ingresar en la caja de texto lo siguiente: solve { 2x - y - 4z = 12, 3x - 4y + 2z = -11, -5x + 2y - z = 2}presionamos enter y la respuesta que obtendremos será la siguiente:

Resolver el siguiente sistema de ecuaciones NO lineales (2x2)

x² - xy = 5

3x +   y  = 1

La solución en video:


La solución online utilizando WolframAlpha:
Debemos ingresar en la caja de texto lo siguiente: solve { x^2 - xy = 5,  3x  + y = 1} presionamos enter y la respuesta que obtendremos será la siguiente:

Solucion de ecuaciones en linea - pagina para resolver ecuaciones lineales - aplicacion online para resolver ecuaciones en linea, programa para resolver ecuaciones online, wolfram alpha en español.